Related Projects: Nitrous Tank (23/24), Nitrous Feed, Nitrous Run Valve
Role: Analyst, Scope Owner
Summary: I wrote a Python script in Fall of 2023 that used REFPROP to simulate nitrous oxide blowdown curves. I then used the results to size the MEOP and volume of the 2023-24 oxidizer tank.
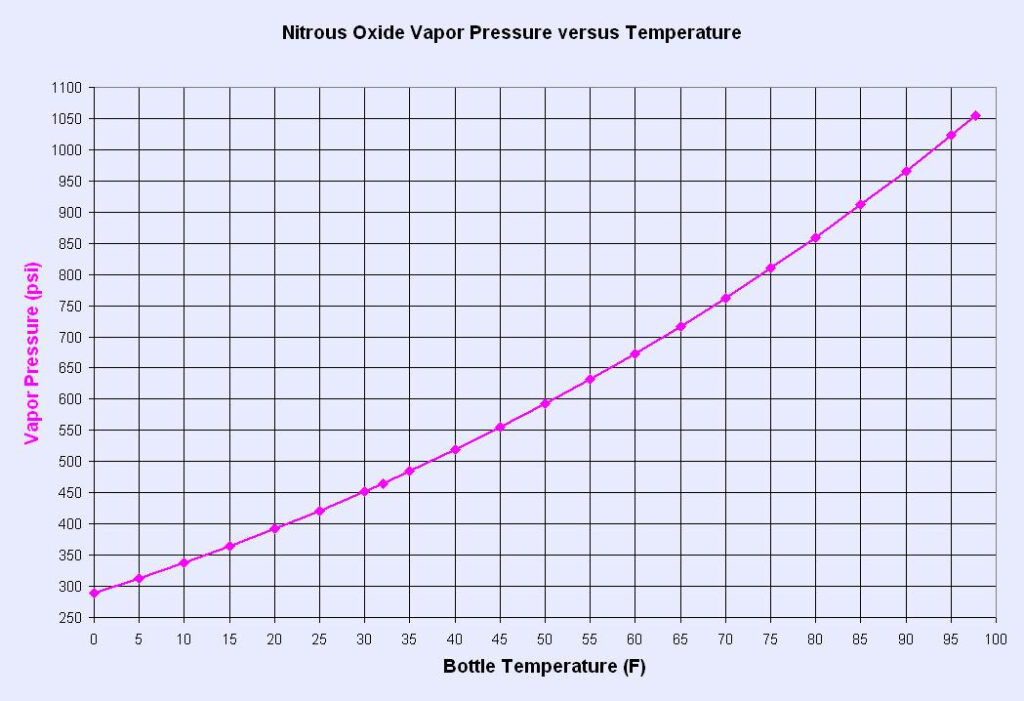
There is an inverse relationship between the density and vapor pressure of nitrous oxide. This modeling effort is intended to select an optimal vapor pressure and density solution to maximize performance and minimize weight in a self-pressurizing blowdown hybrid rocket.
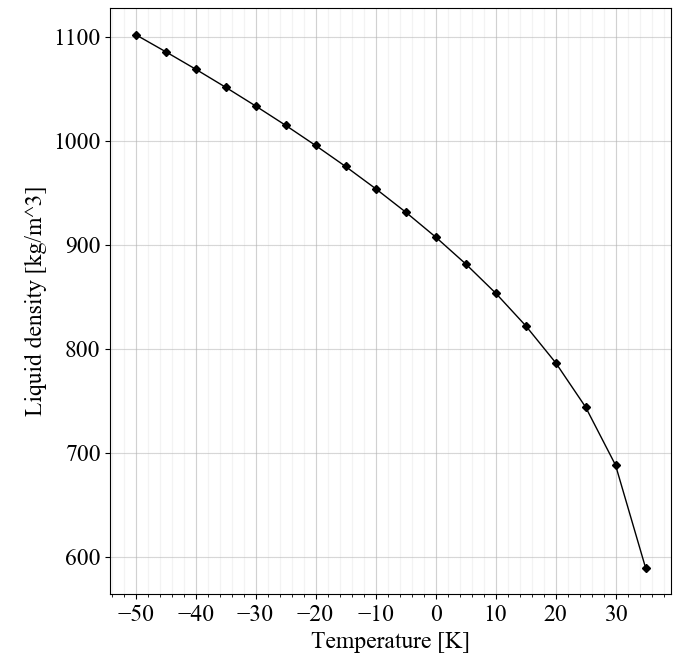
There are diminishing returns to having a higher autogenous vapor pressure. As the density decreases we now need a larger tank, larger valve, and larger plumbing, which add dry mass. A higher dry mass then offsets the higher engine performance, creating an optimal solution to balance those competing factors.
During the blowdown itself, the behavior of the nitrous oxide vapor pressure does not follow that of an inert gas blowdown system. This is because the nitrous oxide is in a saturated equilibrium state while sitting in the tank. I think this might be easiest to explain by analyzing three separate time intervals:
- First interval: The tank is in equilibrium and the vapor pressure is equal to that described by the above tables for a given nitrous oxide temperature. The run valve is opened and the vapor pressure pushes the nitrous out of the tank and into the plumbing/injector.
- Second interval: The tank is no longer in equilibrium because the ullage volume increased as some of the liquid nitrous oxide drained into the injector. This means that the temperature of the liquid nitrous oxide and the vapor pressure in the tank do not agree. Subsequently, some liquid nitrous oxide boils off. However, for some nitrous to boil off the bulk liquid has to lose some thermal energy. This is described by the enthalpy of vaporization.
- Third interval: The tank is returned to equilibrium with slightly lower vapor pressure. After the bulk liquid nitrous loses some thermal energy to the boil-off, its saturation pressure is now lower. This means that the tank pressure will decrease during the burn at a slower rate than standard blowdown.

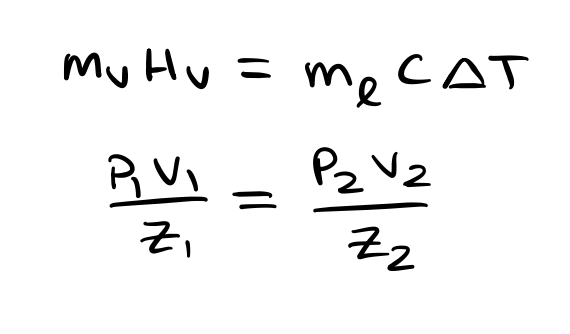
Where Hv is the enthalpy of vaporization, Mv is the nitrous mass that is vaporized, Ml is the liquid mass remaining in the tank, C is the heat capacity of said liquid nitrous, and delta T is the change in temperature as a result of the lost thermal energy to vaporization. P1V1/Z1 = P2V2/Z2 is a modified version of the ideal gas law to account for non-ideal (compressible) fluids.
Applying these principles to a Python program:
To summarize how it works:
- Establish initial parameters: tank size, injector dimensions using Burnell’s semiempirical equation for two-phase flow, initial temperature, and desired time step (improves model fidelity)
- Calculates pre-fire saturation state using the initial parameters and Coolprop wrapper pulling data from REFPROP.
- Performs a loop over tiny time steps. For each time step, a small amount of liquid nitrous is “removed” according to Burnell’s mass flow rate equation. The subsequent vapor pressure is then adjusted.
- For each of these tiny step-downs, it enters another loop that simulates the new pressure and temperature of a tiny amount of nitrous boiling off. It keeps vaporizing this tiny nitrous mass until the temperature and pressure for this time step agree according to the REFPROP saturation table.
- It stores each of these data points in an array, then displays them using Matplotlib.
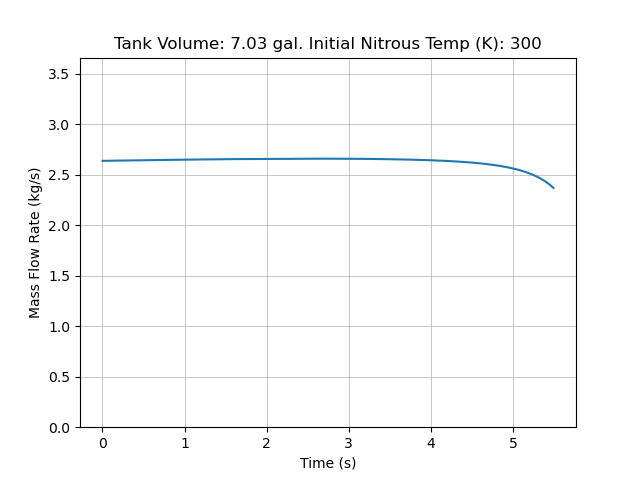
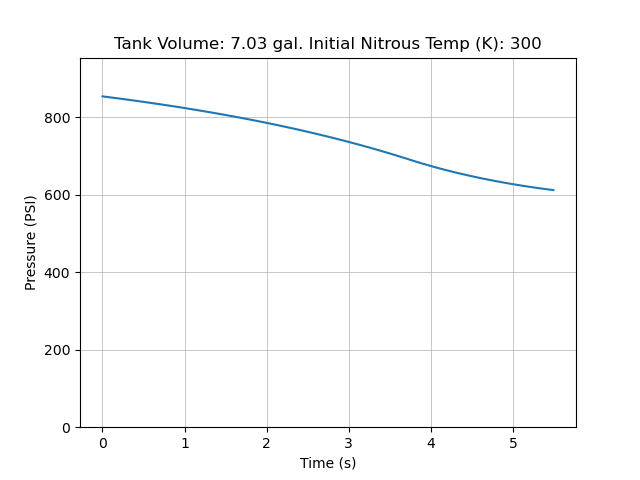
The final results from my code for an extremely small step down:
Compared to data we collected for static fires last year, this is a slight overestimate (~ 50 psi). However, we also had inconsistent load cell readings that year which made it challenging to pinpoint the source of error. Here is static fire data from 4/26/24:
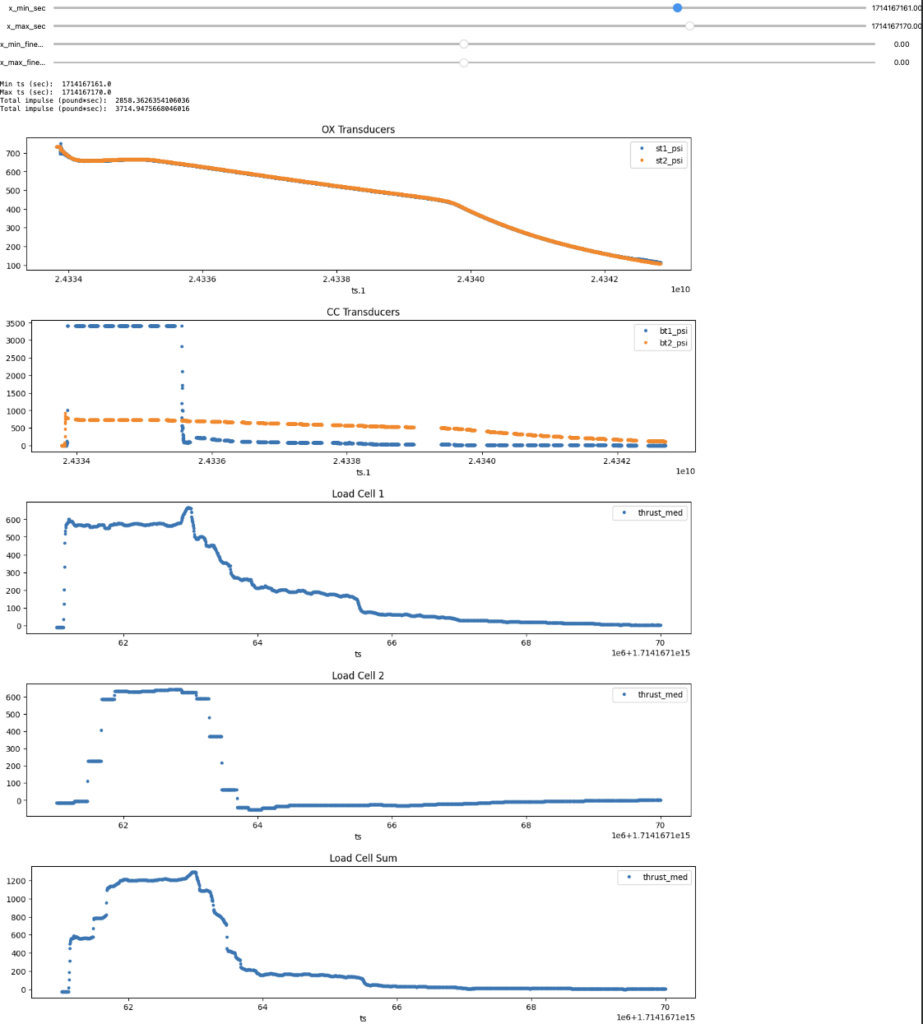
Both the test data and simulation seem to accurately predict the total pressure drop due to cooling of the bulk nitrous, but the test data has a small dip at motor startup and less concavity.