Summary:
I wrote a Python script in Fall of 2023 that used REFPROP fluid properties to calculate nitrous oxide blowdown curves. I then used the results to size the MEOP and volume of the 2023-24 oxidizer tank.
Article:
The goal of this project is to characterize the blowdown vapor pressure and mass flow rate through the injector as a function of burn time, thus arriving at an approximation for the initial vapor pressure necessary for this year’s hybrid rocket motor and making it possible to size the oxidizer tank and plumbing. This will be explained more later, but the higher the vapor pressure the larger the tank, valves, and plumbing need to be to support the same mass flow rate. It’s important these are sized beforehand so we don’t find ourselves with an undersized or oversized system.
Before I explain how my code works, a quick explanation about why tank pressure modeling is necessary:
In a standard blowdown system, the ullage space of a rocket is pressurized with some inert gas, like helium or nitrogen. Then, as the tank empties the gas volume expands and the pressure decreases. For example, a tank with 50% ullage volume filled with 1,000 psi of gas will have ~ 500 psi of pressure after all the propellant is expelled (approximate because of cooling during adiabatic expansion).
Alternatively, in a regulated pressure system, as the tank empties the regulator permits gas flow from a pressurant tank, maintaining constant pressure in the propellant tank. Although the additional tank and regulator adds complexity, it provides constant feed pressure throughout a burn which is ideal for performance.
However, in an blowdown nitrous oxide motor, the head pressure is provided autogenously. A property of nitrous oxide is that its saturated vapor pressure is in the sweet spot for rocketry at slightly above room temperate. This is the saturation curve of nitrous oxide pressure as a function of temperature:
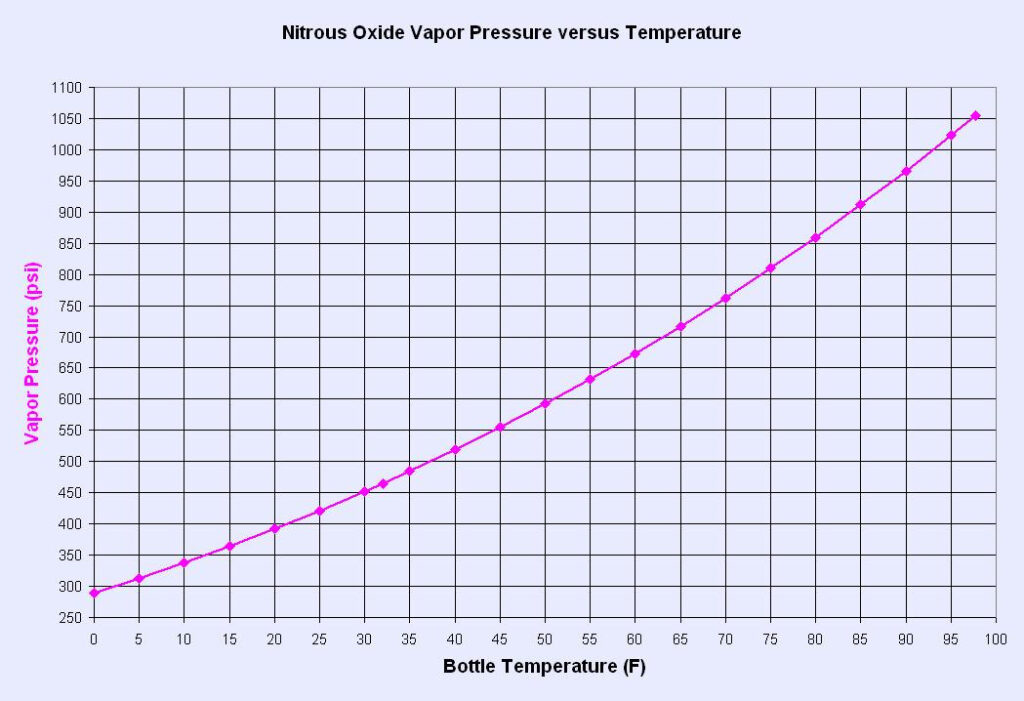
This means that at a temperature of 26.6 degrees Celsius, the nitrous oxide autogenously pressurizes itself to 850 psi. This holds up until its critical pressure, 1055 psi, when nitrous becomes supercritical. However, there’s a trade-off: the nitrous oxide density decreases with temperature as well. Here’s a chart of nitrous oxide density vs. temperature (the liquid and vapor densities converge at the critical point):
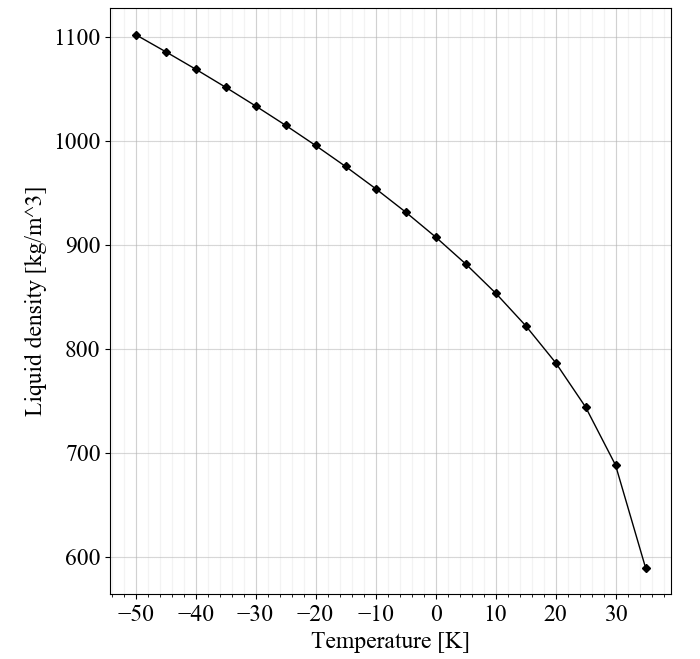
So there are diminishing returns to having a higher autogenous vapor pressure since as the density decreases it means we now need a larger tank, larger valve, and larger plumbing, which add dry mass and subsequently negate the performance benefits of having a higher chamber pressure (which is the main benefit of having a higher vapor pressure). Thus, choosing the vapor pressure carefully is important for optimizing vehicle mass and performance.
During the blowdown itself, the behavior of the nitrous oxide vapor pressure does not follow that of an inert gas blowdown system. This is because the nitrous oxide is in a saturated equilibrium state while sitting in the tank. I think this might be easiest to explain by analyzing three separate time intervals:
- First interval: The tank is in equilibrium and the vapor pressure is equal to that described by the above tables for a given nitrous oxide temperature. The run valve is opened and the vapor pressure pushes the nitrous out of the tank and into the plumbing/injector.
- Second interval: The tank is no longer in equilibrium because the ullage volume increased as some of the liquid nitrous oxide drained into the injector. This means that the temperature of the liquid nitrous oxide and the vapor pressure in the tank do not agree. Subsequently, some liquid nitrous oxide boils off. However, for some nitrous to boil off the bulk liquid has to lose some thermal energy. This is described by the enthalpy of vaporization.
- Third interval: The tank is returned to equilibrium with slightly lower vapor pressure. After the bulk liquid nitrous loses some thermal energy to the boil-off, its saturation pressure is now lower. This means that the tank pressure will decrease during the burn at a slower rate than standard blowdown.

To model this, I had to recall a couple of equations from chemistry:
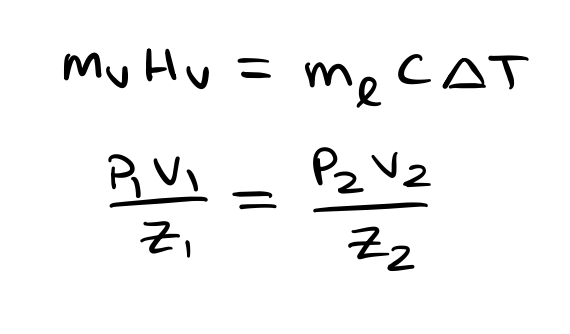
Where Hv is the enthalpy of vaporization, Mv is the nitrous mass that is vaporized, Ml is the liquid mass remaining in the tank, C is the heat capacity of said liquid nitrous, and delta T is the change in temperature as a result of the lost thermal energy to vaporization. P1V1/Z1 = P2V2/Z2 is a modified version of the ideal gas law to account for non-ideal (compressible) fluids.
Finally, to perform the simulation I used a program written in Python. CoolProp has a convenient PropsSI interface that allows me to pull data from REFPROPs libraries. It has two interfaces, a high-level interface with simplified commands and a low-level interface that has higher performance. Because this was the first iteration of this model, I decided to use the high-level interface, however, I plan on optimizing the model in the future to run faster with the low-level interface. [I no longer plan to do this, switching to LOX]
Here’s a pdf of the code I wrote:
To summarize how it works:
- Establish initial parameters: tank size, injector dimensions using Burnell’s semiempirical equation for two-phase flow, initial temperature, and desired time step (improves model fidelity)
- Calculates pre-fire saturation state using the initial parameters and Coolprop wrapper pulling data from REFPROP.
- Performs a loop over tiny time steps. For each time step, a small amount of liquid nitrous is “removed” according to Burnell’s mass flow rate equation. The subsequent vapor pressure is then adjusted.
- For each of these tiny step-downs, it enters another loop that simulates the new pressure and temperature of a tiny amount of nitrous boiling off. It keeps vaporizing this tiny nitrous mass until the temperature and pressure for this time step agree according to the REFPROP saturation table.
- It stores each of these data points in an array, then displays them using Matplotlib.
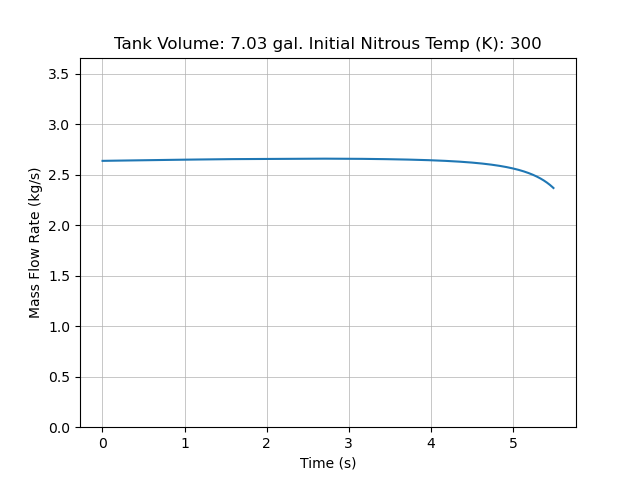
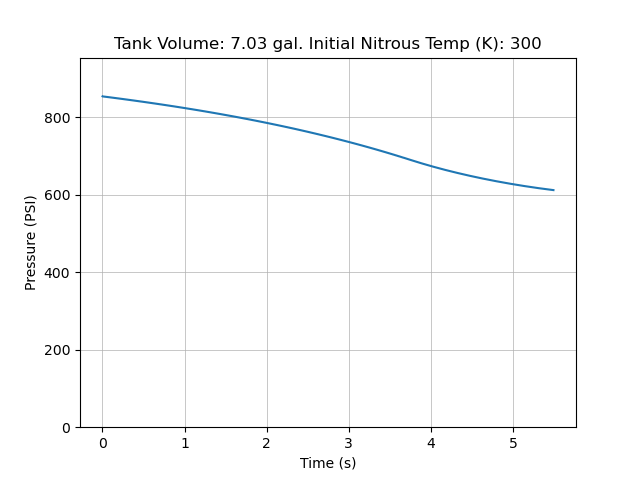
The final results from my code for an extremely small step down:
Compared to data we collected for static fires last year, this is a slight overestimation (~ 50 psi). However, we also had inconsistent load cell readings that year which made it challenging to pinpoint the source of error. Here is static fire data from 4/26/24:
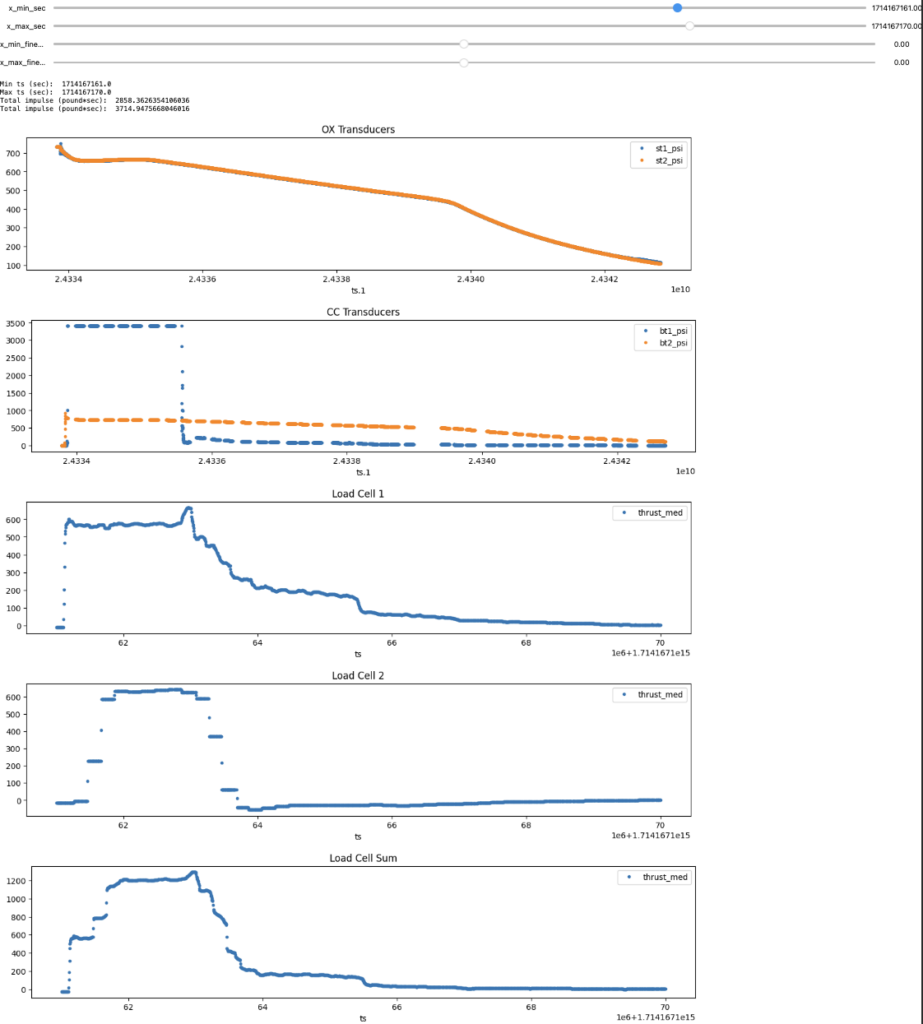
Both the test data and simulation seem to accurately predict the total pressure drop due to cooling of the bulk nitrous, but the test data has a small dip at motor startup and roughly linear behavior, which disagrees with the simulations.
In the future, there are several changes I want to make to this model. The equations for compressibility can definitely be improved with a more complex theoretical model. I also think I can adjust the nested loops to be significantly more efficient by 1. having better variable usage and 2. using the low-level Coolprop interface. This will shorten compile time, so I can increase model fidelity further.